“紧凑度指标”的版本间的差异
来自Wiki.Citydatum
(创建页面,内容为“紧凑度是区域形状特征的一种测度量。相同投影面积的空间由于平面形状不同,反映其空间分布的紧凑程度也不同<ref>《中国土...”) |
小 |
||
| (未显示同一用户的4个中间版本) | |||
| 第1行: | 第1行: | ||
| + | {{提示|该页面还需进一步完善,欢迎加入我们!}} | ||
| + | |||
紧凑度是区域形状特征的一种测度量。相同投影面积的空间由于平面形状不同,反映其空间分布的紧凑程度也不同<ref>《中国土木建筑百科辞典·城市规划与风景园林》</ref>。紧凑度可作为代表城市建成区的紧凑、饱满程度的指标,用于[[城市形态]]的比较与分析。可分为基于长轴的形状率法(Horton,1932;Gibbs,1931)、基于周长的圆形率法(Richardson,1961),以及基于最小外接圆的紧凑度法(Cole,1964)<ref> 李晓江,金晓春,石亚男,翟健,等. 城乡规划编制中的空间分析与辅助决策方法 [M]. 中国建筑工业出版社,2016.</ref>。 | 紧凑度是区域形状特征的一种测度量。相同投影面积的空间由于平面形状不同,反映其空间分布的紧凑程度也不同<ref>《中国土木建筑百科辞典·城市规划与风景园林》</ref>。紧凑度可作为代表城市建成区的紧凑、饱满程度的指标,用于[[城市形态]]的比较与分析。可分为基于长轴的形状率法(Horton,1932;Gibbs,1931)、基于周长的圆形率法(Richardson,1961),以及基于最小外接圆的紧凑度法(Cole,1964)<ref> 李晓江,金晓春,石亚男,翟健,等. 城乡规划编制中的空间分析与辅助决策方法 [M]. 中国建筑工业出版社,2016.</ref>。 | ||
| − | == 形状率紧凑度 == | + | 紧凑度指数(CI, Compaction Index)值的范围在0与1之间,CI越小表示区域形状越不紧凑,越分散。当区域为圆形时,CI为1,为最紧凑形状;当CI趋近于0时,则区域形状接近一条直线,最不紧凑。 |
| − | + | ||
| + | == 数学表达式 == | ||
| + | === 形状率紧凑度 === | ||
| + | 数学表达式:<math height = "30em"> \frac {1.273 \times A} { L^2 } </math> | ||
* A:区域面积; | * A:区域面积; | ||
* L:区域最长轴; | * L:区域最长轴; | ||
| − | == 圆形率紧凑度 == | + | === 圆形率紧凑度 === |
| − | + | 数学表达式1:<math height = "30em"> \frac { 2 \sqrt { \pi A} } { P } </math> | |
| + | 数学表达式2:<math height = "30em"> \frac {4 \pi A} {P^2} </math> | ||
* A:区域面积; | * A:区域面积; | ||
* P:区域周长; | * P:区域周长; | ||
| − | == 外接圆紧凑度 == | + | === 外接圆紧凑度 === |
| − | + | 数学表达式:<math height = "30em"> \frac {A} {A'} </math> | |
* A:区域面积; | * A:区域面积; | ||
* A':最小外接圆面积; | * A':最小外接圆面积; | ||
| + | |||
| + | == 应用实例 == | ||
| + | * 英国学者利用CI研究Ruddington建成区的演变,计算出该区1770年的CI为0.36,1963年时为0.43,表明该城区有集中紧凑发展的趋势。<ref>[https://wenku.baidu.com/view/fe130053af1ffc4ffe47ac66.html 空间分布的测度](百度文库)</ref> | ||
== 参考资料 == | == 参考资料 == | ||
<References /> | <References /> | ||
| + | |||
| + | [[分类:量化指数]] | ||
2018年5月15日 (二) 06:16的最新版本
紧凑度是区域形状特征的一种测度量。相同投影面积的空间由于平面形状不同,反映其空间分布的紧凑程度也不同[1]。紧凑度可作为代表城市建成区的紧凑、饱满程度的指标,用于城市形态的比较与分析。可分为基于长轴的形状率法(Horton,1932;Gibbs,1931)、基于周长的圆形率法(Richardson,1961),以及基于最小外接圆的紧凑度法(Cole,1964)[2]。
紧凑度指数(CI, Compaction Index)值的范围在0与1之间,CI越小表示区域形状越不紧凑,越分散。当区域为圆形时,CI为1,为最紧凑形状;当CI趋近于0时,则区域形状接近一条直线,最不紧凑。
数学表达式
形状率紧凑度
数学表达式: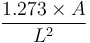
- A:区域面积;
- L:区域最长轴;
圆形率紧凑度
数学表达式1:数学表达式2:
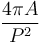
- A:区域面积;
- P:区域周长;
外接圆紧凑度
数学表达式: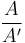
- A:区域面积;
- A':最小外接圆面积;
应用实例
- 英国学者利用CI研究Ruddington建成区的演变,计算出该区1770年的CI为0.36,1963年时为0.43,表明该城区有集中紧凑发展的趋势。[3]